Quick shoutout to Natasha the Robot for her excellent writeup.
“Recursion is one of the most elegant things I don’t fully understand.
”
Recursion is beautiful. It's a bit like the movie Inception, in which everyone is in a dream within a dream.
In other words, a recursive method calls itself with new variables and continues to do so until the problem is solved, the method is told to break or your computer crashes.
It's important to note that while a loop also continues to do something until it's forced to stop, loops are iterators and are not recursive in nature.
Factorials
One of the problems best solved through a recursive method is finding the factorial of a number, which is denoted as the number, followed by an exclamation point (e.g. 5!).
Factorial Iteration vs. Recursion
When I first approached the problem, I kept fighting the urge to iterate over the numbers. I blame Ruby's excellent flexibility.
While you can find the factorial of a number, it's more elegantly coded as a recursive method.
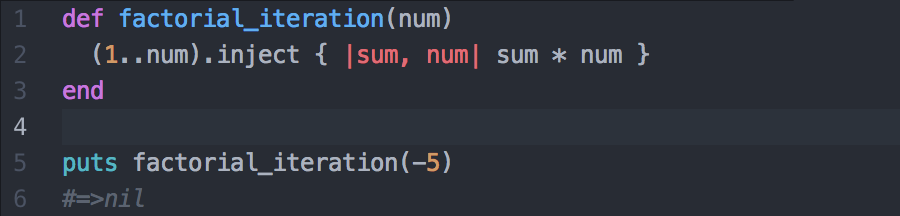
Nevertheless, here's an example of how you could iterate to find the factorial of a number:
You can read more about the #inject method in the Ruby docs.
Potential Problems
Negative numbers
Factorials of negative numbers are undefined. (I'm not a mathematician, but you can read more about there here.)
When I create a recursive method that takes input from the user, I'll have to make sure they submit a positive integer or natural number (in this case, I'm including zero as a natural number).
The iteration currently doesn't account for this. It simply returns nil.
ZERO
The factorial of zero is one (0! = 1). If that's confusing to you, as it was to me, here's a brief explanation.
1! = 1
2! = 2
3! = 6
4! = 24
If you're thinking, "Well, duh, get to the point," bear with me.
Let's take a different approach.
3! = 4!/4
In other words, 3! = 24/4, which can be further simplified to 3! = 6.
OK, awesome. Let's do the rest.
2! = 3!/3 = 2
1! = 2!/2 = 1
Here's the kicker:
0! = 1!/1 = 1
Neat, huh? So, if the user inputs zero, I'll have to ensure the method returns one. The iteration below doesn't account for this.
Getting Started
I wrote some pseudocode of what I wanted to accomplish before I started coding.
START program GET input from user, convert string to integer IF input == 0, RETURN 1 LOOP IF input < 0, ask user for another input END LOOP RETURN factorial of input END program
User prompt method
I created a simple method to add "=> " in front of any message. It will allow the user to more easily see messages and prevent me from having a hundred `puts` in my program.
Welcome to Factorial!
I started the program off with a simple welcome message and asked the user to input a positive integer.
User Input + Verification
I had to define the variable outside of the loop, so I set `user_input` to zero.
When the user inputs a number, I convert it to an integer and check if it's a number greater than zero using the `is_valid?` method.
If the number is negative, `is_valid?` returns a false and the loop tells the user it's not a valid number.
stack level too deep
If you allowed the user to input a negative number using this recursive method, it wouldn't return nil.
Instead, it would return an error: stack level too deep (SystemStackError).
Though it returns the error within a second, the computer can't process the amount of information you've put on top of the memory stack.
Basically, you've asked it to compute too much information and it's politely saying no.
Recursive Method
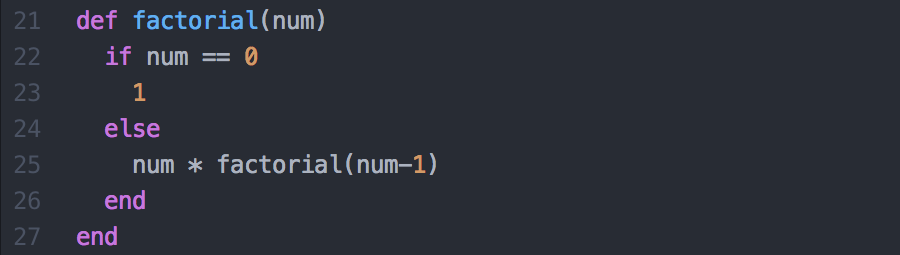
And now the fun part. First, the `factorial` method determines if `user_input` is equal to zero. If it is, it returns a one.
If it's not, it begins recursively problem-solving.
As you can see above, the recursive method takes a number and multiplies it by the recursive method minus one.
Visualizing Recursion
Returning the factorial
The final step is to let the user know the factorial of the value they inputed.